理解简谱中记录的旋律

前言

本文仅用于整理笔者在查阅资料后对简谱这一记谱方式的简单理解，其主要服务于本人的课程设计（需要使用蜂鸣器或其它电子元件简单演奏简谱中的旋律），不涉及任何复杂的知识（如和弦、泛音等）。由于本人从未学习过乐理知识，错误在所难免，欢迎指正。如果对您造成了误导的话，那咱也不能负责捏～橙子什么都不知道哦～

音高相关

音符

简谱使用 1 ～ 7 七个数字来表示音符，分别对应了自然大调的七个音阶。

这七个音符位于一个八度，当需要高于或低于这个八度的音符时，可以在数字上方或下方加上一个点（或多个点）表示升高或降低一个八度。

同一个音符在不同的八度中，音高不同。如果用物理声学的方式表达，那么相隔一个八度的两个音符的频率比为 2:1。例如，如果我们规定中音的 La ($6$) 为 440Hz，那么高音的 La ($\overset{\cdot}{6}$) 为 880Hz，低音的 La ($\underset{\cdot}{6}$) 为 220Hz。

在十二平均律（现代钢琴使用的就是这种律制）中，每个八度以等比例的方式分为 12 个半音，相邻两个半音的频率比为 $\sqrt[2]{12} = 2^{\frac{1}{12}}$。而自然大调音阶满足“全-全-半-全-全-全-半”的音程规律，即：

音名

音名就是音高的名称，每个音名对应了一个绝对的音高（即有一个确定的频率）。科学音高记号（SPN）是常用于键盘乐器的一种表示方法，使用 $C, C\sharp=D\flat, D, D\sharp=E\flat, E, F, F\sharp=G\flat, G, G\sharp=A\flat, A, A\sharp=B\flat, B$ 来表示一个八度中的 12 个半音，并通过添加数字表示这个音名所在的八度（音区）：$C_0, C_1, C_2, \cdots, C_{10}$。在这种记号下，中央 C 被表示为 $C_4$。

现代音乐通常规定，$A_4$ 的音高为 440Hz，通过十二平均律，我们可以计算出其它音名的音高，例如：

调号

简谱使用首调唱名法，通过简谱左上角的调号来确定主音。
例如，使用 $1 = C$ 来表示主音，此时 Do (1) 为 $C$。再如，使用 $1 = F\sharp$ 来表示主音，此时 Do (1) 为 $F\sharp$。其它音符的音高可以通过自然大调的音程规律和十二平均律来计算。

注意：简谱并不确定主音具体位于哪个八度（音区）。在使用简谱时，需要根据实际情况确定主音所在的八度。使用不同乐器演奏或不同音高的演唱者演唱时，主音所在的八度可能会有所不同。

实例

下面是一个简谱的例子：

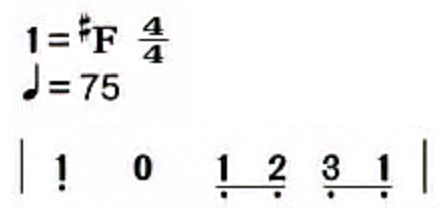
这个简谱的调号是 $1 = F\sharp$，假设取中音的 Do (1) 为 $F_5\sharp$。其 6 个音符对应的音名分别为：

音长相关

音乐速度（BPM）

音乐速度以 BPM（Beats Per Minute）为单位，表示每分钟的拍数。例如，$120 \text{BPM}$ 表示每分钟有 120 拍，此时每拍的时值为 $\frac{60}{120} = 0.5$ 秒。

BPM 一般标记在简谱左上角（例如：𝅘𝅥 = 75），也可能使用文字描述（例如：急促地）。

拍号

简谱的拍号往往紧跟在调号之后，以 $\frac{2}{4}$ 的格式表示，横线上方表示每小节的拍数，横线下方表示每拍的时值。例如:

• $\frac{2}{4}$ 表示每小节有 2 拍，每拍为四分音符。
• $\frac{4}{4}$ 表示每小节有 4 拍，每拍为四分音符。

音符时值

简谱中，单独一个数字表示四分音符，数字下方加一个短横表示八分音符，数字下方加两个短横表示十六分音符，以此类推。例如：

• $1$ 表示四分音符
• $\underline{1}$ 表示八分音符
• $\underline{\underline{1}}$ 表示十六分音符

数字后面加横线表示延长音符，每个横线表示延长一个四分音符的时值，例如：

• $1\text{\ \textendash}$ 表示二分音符
• $1\text{\ \textendash\ \textendash\ \textendash}$ 表示全音符。

同时，在简谱中，还可以使用附点来延长音符时值。附点表示在原有时值上增加一半的时值。例如：

• $1\cdot$ 表示 $\frac{1}{4} + \frac{1}{8}$ 个全音符的时值
• $\underline{1}\cdot$ 表示 $\frac{1}{8} + \frac{1}{16}$ 个全音符的时值
• $\underline{1}\cdot\cdot$ 表示 $\frac{1}{8} + \frac{1}{16} + \frac{1}{32}$ 个全音符的时值

附录：音名与频率对照表

参考资料

Wikipedia: Scientific pitch notation
Wikipedia: 简谱